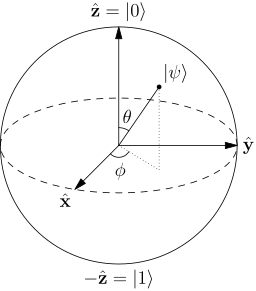
Note: The qubit is a two-state system which can be in a superpositional state analogous to Youngs classical experiment (Østgård et al., 2014).
The qubit requires a completely new way of thinking about information and computation. A qubit is a two-level quantum mechanical system and it can be in a superpositional state, i.e., multiple states at the same time. Mathematically, a quantum logical qubit state can be written as a linear combination (viz., superposition) of |0⟩ and |1⟩.
Dirac notation of a superpositional state:
\({\displaystyle |\psi \rangle =\alpha |0\rangle +\beta |1\rangle ,\,}\)
Moreover, a qubit can be visually represented as a Bloch sphere which is eponymously named after its inventor (Bloch, 1946). Fascinatingly, a single qubit can in principle carry the information of all libraries in the world (Muthukrishnan & Stroud, 2000), viz., continuous-valued quantum information in a linear superposition (the problem is how to measure the information without destroying it via collapse of the superposition caused by the measurement).
Computational modelling in psychology and neuroscience
All known information processing systems are physically embodied (i.e., they are grounded in physical substrates). From a reductionist point of view, the underlying physics of all information processing systems is consequently ultimately quantum-mechanical in nature. It follows deductively that science has to reconsider information processing and computation in the light of recent evidence from quantum physics. Information processing and computation play a major role in psychology, neuroscience, and many other scientific disciplines (e.g., computational cognitive science (Sun, 1950), computational neuroscience (Sejnowski, Koch, & Churchland, 1988), computational biology , etc. pp.). For instance, cognitive modelling is concerned with computational models of cognition. These models assume “cognitive completeness” (Yearsley & Pothos, 2014). Cognitive completeness implies that behaviour (e.g., perceptual judgments) can be explained in purely cognitive terms without the invocation of neural correlates. This is an implicit assumption of almost all cognitive models, otherwise cognitive science would be forced to constantly integrate the complexities of neurophysiology and neurochemistry into its modelling efforts (of course there are exception). In sensu lato, cognitive completeness is embedded in the notion of “multiple levels of description and explanation” (Coltheart, 2010; Perfors, 2012). In the last century, quantum physics discovered extraordinary phenomena which shed new light on the fundamental workings of reality.
Superposition is an essential property which is utilised for quantum computation and it also appears to be applicable to models of cognition (Busemeyer & Bruza, 2012). Moreover, the future of the rapidly developing fields of machine learning and artificial intelligence is likely based on these extremely powerful quantum computational principles which require a radically new way to think about information (Biamonte et al., 2017; Dunjko & Briegel, 2017; Prati, 2017). Therefore, cognitive psychology is now carrying the burden of proof: Why should nature not make use of these extremely effective quantum-principles in the domain of cognitive processes? Most models of cognition are strongly influenced by the principles of digital binary computation (Piccinini & Bahar, 2013), although some argue that “cognition is not computation”62 (Bringsjord & Zenzen, 1997). A classical bit can adopt two possible states (i.e., binary states) usually symbolised as 0 and 1 (but more generally “true” or “false” or any other dichotomous notation, e.g., cats and dogs, as the physical substrate in which the bit is realised is not important. This substrate independence is known as multiple realizability, for a discussion of this fundamental concept see Shapiro (2000). This implies that computation should be treated as logical abstraction – what is important is software (logic) not the physical substrate (hardware).
Alan Turing wrote:
“The [Babbage Engine’s] storage was to be purely mechanical, using wheels and cards. The fact that Babbage’s Analytical Engine was to be entirely mechanical will help us rid ourselves of a superstition. Importance is often attached to the fact that modern digital computers are electrical, and the nervous system is also electrical. Since Babbage’s machine was not electrical, and since all digital computers are in a sense equivalent, we see that this use of electricity cannot be of theoretical importance. … If we wish to find such similarities we should look rather for mathematical analogies of function.”
Richard Feynman argued in his lecture series on quantum computation that Turing’s arguments were impeccable but that he did not consider substrates that behave according to the “strange” laws of quantum logic. The crucial point is that it has become very clear that classical notions of physics are no longer defendable on empirical grounds (e.g., local realism) (Giustina et al., 2015; Hensen et al., 2015; Wiseman, 2015). All information processing systems are embodied in some form of physical substrate. Given that those physical substrates ae governed by the laws of quantum mechanics, it follows that classical (Newtonian) notions of computation have to be revised (and in fact are currently being revised) in the light of insight derived from quantum physics. For instance, Google and NASA are currently heavily investing into quantum computation and quantum AI (both are grounded on quantum logic). In sum, quantum computational principles will significantly speed up a large array of computational processes (Rønnow et al., 2014) and might turn out to be a driving force for the continuation of Moore’s law (Lundstrom, 2003; G. E. Moore, 1965). Superposition and entanglement are pivotal concepts in quantum information and quantum computing (Boyer, Liss, & Mor, 2017). Quantum information and computation are closely related to quantum cognition, as cognition is understood to be information processing. Many cognitive and neuroscientists believe that cognition is essentially a form of computational, i.e., it can be modelled mathematically by utilising various computational principles (i.e., Bayes’ rule). Therefore, it is obvious that cognitive scientists should consider quantum computational principles which do not obey Bayes’ rule (which is based on Kolmogorov’s probability axioms). The same quantum computational principles are also important for neuroscience and particularly (neuro)computational neuroscience and artificial intelligence. Currently, neurons are almost exclusively modelled as binary states (firing vs. resting), even though several researchers are now beginning to integrate quantum approaches into their efforts (Schuld, Sinayskiy, & Petruccione, 2014). From a quantum perspective, neurons can be modelled as superpositional states. Given that neurons are thought to underpin all of cognition (at least in a reductionist materialism framework) this has implications for the high-order cognitive processes and computational models of cognition which are based on these neurocomputational processes.